Difference between revisions of "Research"
(No difference)
|
Revision as of 16:39, 17 October 2021
"You see things; and you say, 'Why?' But I dream things that never were; and I say, 'Why not?'"–– George Bernard Shaw (1856 –1950)
Our research spans different disciplines ranging from digital circuit design, to algorithms, to mathematics, to synthetic biology. It tends to be inductive (as opposed to deductive) and conceptual (as opposed to applied). A recurring theme is building systems that compute in novel or unexpected ways with new and emerging technologies. Often, the task of analyzing the way things work in a new technology is straightforward; however the task of synthesizing new computational constructs is more challenging.
Computing with Random Bit Streams
"To invent, all you need is a pile of junk and a good imagination." –– Thomas A. Edison (1847–1931)
Humans are accustomed to counting in a positional number system – decimal radix. Nearly all computer systems operate on another positional number system – binary radix. From the standpoint of representation, such positional systems are compact: given a radix b, one can represent bn distinct numbers with n digits. However, from the standpoint of computation, positional systems impose a burden: for each operation such as addition or multiplication, the signal must be "decoded", with each digit weighted according to its position. The result must be "encoded" back in positional form. Any student who has designed a binary multiplier in a course on logic design can appreciate all the complexity that goes into wiring up such an operation.
Logic that Operates on Probabilities
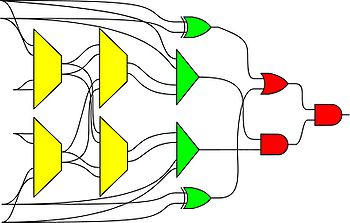
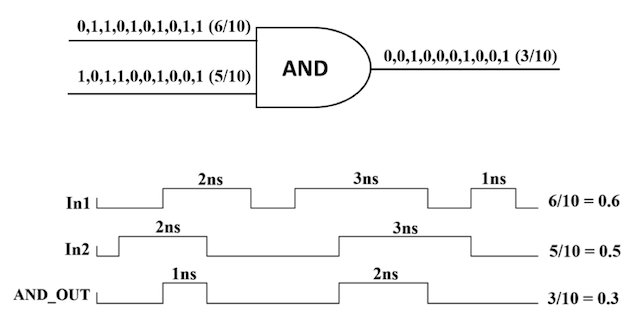
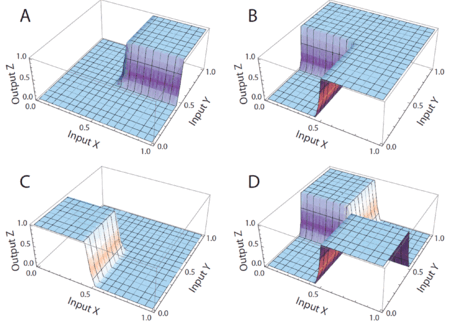
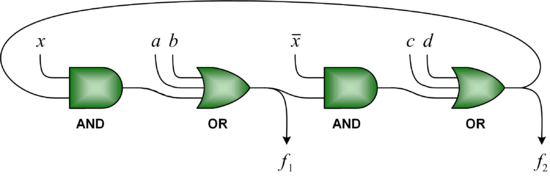
We advocate an alternative representation: random bit streams where the signal value is encoded by the probability of obtaining a one versus a zero. This representation is much less compact than binary radix. However, complex operations can be performed with very simple logic. For instance, multiplication can be performed with a single AND gate; scaled addition can be performed with a multiplexer (MUX).
We have developed a general method for synthesizing digital circuitry that computes on such stochastic bit streams. Our method can be used to synthesize arbitrary polynomial functions. Through polynomial approximations, it can also be used to synthesize non-polynomial functions. Because the representation is uniform, with all bits weighted equally, the resulting circuits are highly tolerant of soft errors (i.e., bit flips).
|
|
Logic that Generates Probabilities
Schemes for probabilistic computation can exploit physical sources to generate random values in the form of bit streams. Generally, each source has a fixed bias and so provides bits that have a specific probability of being one versus zero. If many different probability values are required, it can be difficult or expensive to generate all of these directly from physical sources. In this work, we demonstrate novel techniques for synthesizing combinational logic that transforms a set of source probabilities into different target probabilities.
|
Computing with Crappy Clocks
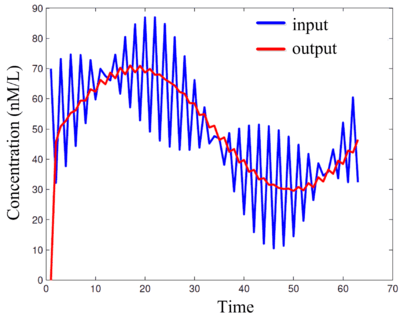
Clock distribution networks are a significant source of power consumption and a major design bottleneck for high-performance circuits. We have proposed a radically new approach: splitting clock domains at a very fine level, with domains consisting of only a handful of gates each. These domains are synchrnonized by "crappy clocks", generated locally with inverter rings. This is feasible if one adopts the paradigm of computing on randomized bit streams.
|
Please see our "Publications" page for more of our papers on these topics.
Computing with Molecules
“If I can’t create it, I don’t understand it.” –– Richard Feynman (1918–1988)
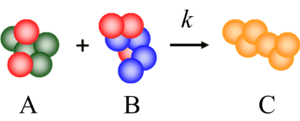
The theory of mass-action kinetics underpins our understanding of biological and chemical systems. It is a simple and elegant formalism: molecular reactions define rules according to which reactants form products; each rule fires at a rate that is proportional to the quantities of the corresponding reactants that are present. Just as electronic systems implement computation in terms of voltage (energy per unit charge), we can conceive of molecular systems that compute in terms of chemical concentrations (molecules per unit volume). We are studying techniques for implementing a variety of computational constructs with molecular reactions such as logic, memory, arithmetic, and signal processing. Although conceptual, we target DNA Strand Displacement as our experimental chassis.
|
|
 We map abstract molecular reactions to DNA reactions. Through a process called DNA strand displacement, single strands of DNA displace parts of double strands, releasing other single strands. |
Computational Constructs
We have developed a strategy for implementing digital logic with molecular reactions. Based on a bistable mechanism for representing bits, we implement a constituent set of logical components, including combinational components such as AND, OR, and XOR gates, as well as sequential components such as D latches and D flip-flops. Using these components, we build full-fledged digital circuits such as a binary counters and linear feedback shift registers.
|
We have developed a strategy for implementing arithmetic with molecular reactions – operations such as increments & decrements, multiplication, logarithms, and exponentiation. Try out our compiler: it translates arbitrary constructs from a C-like language into a robust implementation with molecular reactions.
|
We have developed a strategy for implementing signal processing with molecular reactions including operations such as filtering. We have demonstrated robust designs for Finite-Impulse Response (FIR), Infinite-Impulse Response (IIR) filters, and Fast Fourier Transforms (FFTs).
|
|
|
The impetus for this research is not computation per se. Molecular computation will never compete with conventional computers made of silicon integrated circuits for tasks such as number crunching. Chemical systems are inherently slow and messy, taking minutes or even hours to finish, and producing fragmented results. Rather, the goal is to create “embedded controllers” – viruses and bacteria that are engineered to perform useful molecular computation in situ where it is needed, for instance for drug delivery and biochemical sensing.
Please see our "Publications" page for more of our papers on these topics.
Computational Immunology
“Biology is the study of the complex things in the Universe. Physics is the study of the simple ones.” –– Richard Dawkins (1941– )
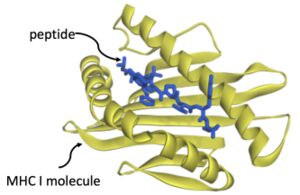
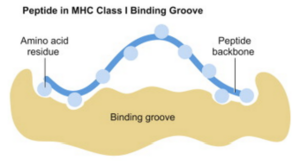
Cellular immunity allows circulating T-cells to kill off infected cells. When a cell is infected with a virus, it hijacks the host cell’s machinery, forcing it to make viral proteins. Our cells have a defense mechanism: they chop up such proteins into fragments, called peptides, and transport them to the cell surface, bound to MHC I molecules. Presented this way on the cell surface, T-cells can identify a cell as being infected and can destroy it using toxins. If this mechanism succeeds, an infection is stopped in its tracks: T-cells kill off infected cells before they can do damage. If it fails, then infected cells become factories for reproducing copies of the virus and full-blown disease results.
|
|
Machine Learning Predictions
Predicting peptide-MHC binding is of significance in determining whether a given person's immune system can detect and effectively respond to cellular infections. NetMHC and NetMHCpan are state-of-the-art machine learning based tools used for this purpose. While investigating binding peptides predicted from the SARS-Cov-2 spike protein, we observed certain false positives being predicted as binders. We identified hydrophobicity as a key biochemical factor that was useful for testing the accuracy of these machine learning predictions.
|
Mechanistic Simulations
We are currently building a FORTRAN based simulation tool that will model peptide and MHC Class I binding mechanistically, i.e. we will incorporate several biochemical factors pertinent to binding, such as hydrophobicity, van der Waals forces, electrostatic forces, pi-interactions, etc. This work is in collaboration with the Mayo Clinic.
Computing with Nanoscale Lattices
"Listen to the technology; find out what it’s telling you.” –– Carver Mead (1934– )
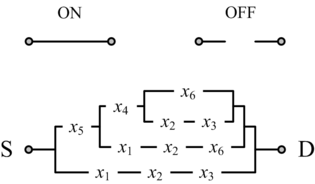
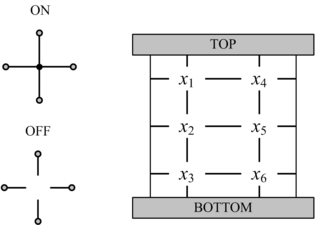
In his seminal Master's Thesis, Claude Shannon made the connection between Boolean algebra and switching circuits. He considered two-terminal switches corresponding to electromagnetic relays. A Boolean function can be implemented in terms of connectivity across a network of switches, often arranged in a series/parallel configuration. We have developed a method for synthesizing Boolean functions with networks of four-terminal switches. Our model is applicable for variety of nanoscale technologies, such as nanowire crossbar arrays, as molecular switch-based structures.
|
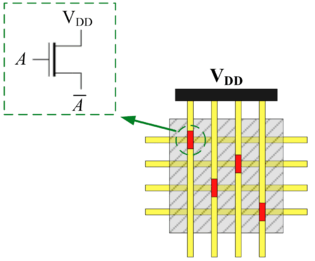
The impetus for nanowire-based technology is the potential density, scalability and manufacturability. Many other novel and emerging technologies fit the general model of four-terminal switches. For instance, researchers are investigating spin waves. A common feature of many emerging technologies for switching networks is that they exhibit high defect rates.
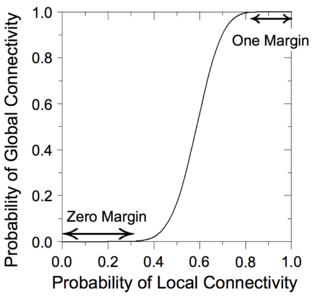
We have devised a novel framework for digital computation with lattices of nanoscale switches with high defect rates, based on the mathematical phenomenon of percolation. With random connectivity, percolation gives rise to a sharp non-linearity in the probability of global connectivity as a function of the probability of local connectivity. We exploit this phenomenon to compute Boolean functions robustly in the presence of defects.
|
Please see our "Publications" page for more of our papers on these topics.
Computing with Feedback
"A person with a new idea is a crank until the idea succeeds." –– Mark Twain (1835–1910)
The accepted wisdom is that combinational circuits (i.e., memoryless circuits) must have acyclic (i.e., loop-free or feed-forward) topologies. And yet simple examples suggest that this need not be so. We advocate the design of cyclic combinational circuits (i.e., circuits with loops or feedback paths). We have proposed a methodology for synthesizing such circuits and demonstrated that it produces significant improvements in area and in delay.
|
Please see our Publications page for more of our papers on this topic.
Algorithms and Data Structures
"There are two kinds of people in the world: those who divide the world into two kinds of people, and those who don't." –– Robert Charles Benchley (1889–1945)
Consider the task of designing a digital circuit with 256 inputs. From a mathematical standpoint, such a circuit performs mappings from a space of Boolean input values to Boolean output values. (The number of rows in a truth table for such a function is approximately equal to the number of atoms in the universe – rows versus atoms!) Verifying such a function, let alone designing the corresponding circuit, would seem to be an intractable problem. Circuit designers have succeeded in their endeavor largely as a result of innovations in the data structures and algorithms used to represent and manipulate Boolean functions. We have developed novel, efficient techniques for synthesizing functional dependencies based on so-called SAT-solving algorithms. We use Craig Interpolation to generate circuits from the corresponding Boolean functions.
|
Please see our "Publications" page for more of our papers on this topic. (Papers on SAT-based circuit verification, that is, not on squids.)
Mathematics
"Mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true." –– Bertrand Russell (1872–1970)
The great mathematician John von Neumann articulated the view that research should never meander too far down theoretical paths; it should always be guided by potential applications. This view was not based on concerns about the relevance of his profession; rather, in his judgment, real-world applications give rise to the most interesting problems for mathematicians to tackle. At their core, most of our research contributions are mathematical contributions. The tools of our trade are discrete math, including combinatorics and probability theory.

|
Please see our "Publications" page for more of our papers on this topic.
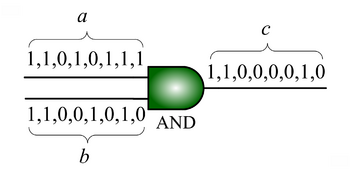
 that is the product of the of the input probabilities
that is the product of the of the input probabilities  and
and  .
.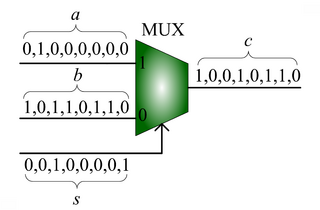
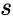 , the MUX produces an output probability
, the MUX produces an output probability 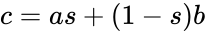 .
.



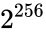 Boolean input values to Boolean output values. (The number of rows in a
Boolean input values to Boolean output values. (The number of rows in a 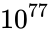 rows versus
rows versus 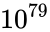 atoms!) Verifying such a function, let alone designing the corresponding circuit, would seem to be an intractable problem. Circuit designers have succeeded in their endeavor largely as a result of innovations in the data structures and algorithms used to represent and manipulate
atoms!) Verifying such a function, let alone designing the corresponding circuit, would seem to be an intractable problem. Circuit designers have succeeded in their endeavor largely as a result of innovations in the data structures and algorithms used to represent and manipulate